Asymmetric cryptography uses different keys for encrypting and decrypting data. The key used for encryption is called the public key, and the key used for decryption is called the private key.
Asymmetric cryptography schemes are used for secure communication over insecure channels, such as the internet. It is used in blockchain networks for users to sign transactions and prove ownership over funds and accounts.
- How Asymmetric Cryptography Works?
- Asymmetric Cryptography In Blockchains
- ECDSA Cryptography In Practice
How Asymmetric Cryptography Works?
Asymmetric cryptography relies on complex mathematical concepts, such as modular arithmetic, sets, groups, cyclic groups, and fields. These mathematical concepts are used to perform encryption and decryption allowing a private key holder to sign a transaction and send it along with their public key. Any 3rd party can verify that the owner of the public key also knows the private key to generate a valid signature.
A private key is a randomly generated number that is kept secret and held privately by its users. Private keys need to be protected and no unauthorized access should be granted to those keys.
A public key is freely available and published by the private key owner. Anyone who would like to send an encrypted message to the publisher of the public key can do so, by encrypting the message using the published public key and sending it to the holder of the private key. Once the public key-encrypted message is received, the recipient can decrypt the message using the private key.
The security of asymmetric cryptography schemes relies on the difficulty of certain mathematical problems, such as factoring large composite numbers or finding the discrete logarithm of a random elliptic curve point. This difficulty makes it infeasible to derive the private key from the public key.
Asymmetric Cryptography In Blockchains
Asymmetric cryptography is a fundamental component in blockchains and cryptocurrencies, as it allows for secure transactions and the verification of data integrity without the need for a trusted third party.
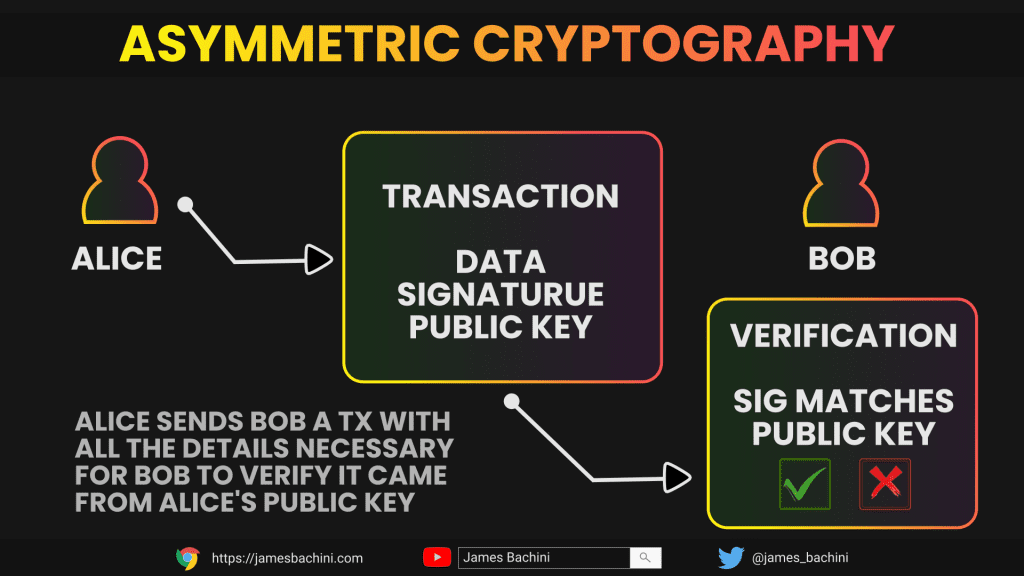
Each user has a pair of public and private keys. The user’s wallet address is either the public key itself or a derivative of this key, which is used to receive funds. The private key is used to sign transactions and transfer funds from the user’s account. When a user initiates a transaction, they sign it using their private key, and the transaction is broadcast to the network for verification and processing.
Once the transaction is received by the network it is validated by nodes. The transaction includes the sender’s public key, which is used to verify that the transaction is legitimate and that the funds being transferred belong to the sender.
In the blockchain sector we generally use a type of asymmetric cryptography called ECDSA cryptography.
ECDSA Cryptography In Practice
ECDSA (Elliptic Curve Digital Signature Algorithm) is a type of asymmetric cryptography that is commonly used to secure transactions in blockchain applications. It works in 3 stages:
Key Generation The first step in ECDSA is to generate a public-private key pair. This is done by selecting an elliptic curve and a point on that curve, known as the base point. The private key is a randomly generated number, while the public key is derived from the private key using a mathematical formula.
Signature Generation When a user wants to sign a message or transaction, they use their private key to generate a unique signature. The signature is created by performing a series of mathematical calculations using the private key and the message being signed.
Signature Verification To verify the signature, the recipient which is a node on the blockchain network, uses the sender’s public key and the message to perform a similar set of calculations. If the result matches the signature, then the signature is considered valid.
ECDSA is based on the mathematical properties of elliptic curves, which make it difficult to determine the private key based on knowledge of the public key. This makes ECDSA a secure way to sign and verify transactions, as long as the private key remains secret.


