Merkle trees are a useful tool for blockchain developers offering a myriad of benefits, chief among them being the efficient verification of large data sets and proof of inclusion.
By leveraging Merkle trees developers can significantly optimise gas costs and enhance the overall performance of their decentralised applications. In this article we will look at three case studies where Merkle trees are used in the blockchain sector.
- What Are Merkle Trees Good For
- Case Study 1. Merkle Trees For Airdrops
- Case Study 2. Merkle Trees In Voting Mechanisms
- Case Study 3. Merkle Trees In Layer 2 Rollups
What Are Merkle Trees Good For
At their core, Merkle trees excel in providing a compact representation of extensive data sets. This characteristic proves invaluable when dealing with the constraints of blockchain environments.
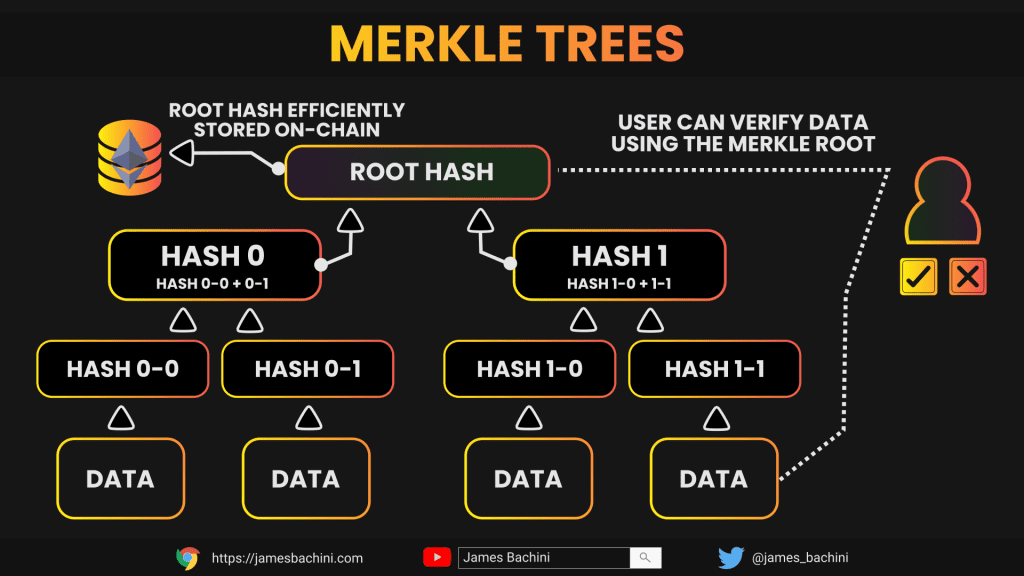
By allowing for the verification of data integrity without the need to store or transmit the entire dataset, Merkle trees enable efficient proof of inclusion mechanisms.
In smart contracts, this translates to reduced on-chain storage requirements and lower gas costs for operations involving large amounts of data. This provides us with the ability to verify the inclusion of a specific piece of data within a larger set, without processing the entire set.
Case Study 1. Merkle Trees For Airdrops
Airdrops have become a popular method for distributing tokens to a large number of recipients in the cryptocurrency space. However, handling these distributions efficiently and securely poses significant challenges. Implementing airdrops naively would require storing extensive lists of recipients on-chain, leading to high gas costs and potential security risks.
By utilising Merkle trees, a more efficient mechanism can be established. The list of eligible recipients is organised into a Merkle tree, and only the Merkle root is stored on-chain. Participants can then claim their tokens by providing a Merkle proof that verifies their inclusion in the distribution list. This approach significantly reduces on-chain data storage requirements and associated costs.
Below is a simplified example of how Merkle trees can be used for airdrops in Solidity:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
import "@openzeppelin/contracts/utils/cryptography/MerkleProof.sol";
contract MerkleAirdrop {
bytes32 public merkleRoot;
mapping(address => bool) public hasClaimed;
constructor(bytes32 _merkleRoot) {
merkleRoot = _merkleRoot;
}
function claimTokens(bytes32[] calldata merkleProof) external {
require(!hasClaimed[msg.sender], "Tokens already claimed");
bytes32 leaf = keccak256(abi.encodePacked(msg.sender));
require(
MerkleProof.verify(merkleProof, merkleRoot, leaf),
"Invalid Merkle proof"
);
hasClaimed[msg.sender] = true;
// Transfer tokens to the sender
// token.transfer(msg.sender, amount);
}
}
In this contract we are using the OpenZeppelin MerkleProof.sol library. In the constructor function we store the root of the Merkle tree representing all eligible recipients along with a map to track if an address has already claimed their tokens.
We then create a function that allows users to claim their tokens by providing a Merkle proof.
Participants generate a Merkle proof off-chain and submit it along with their claim. The contract verifies the proof without needing to store the entire list of recipients on-chain.
Case Study 2. Merkle Trees In Voting Mechanisms
Secure and transparent voting systems are crucial for the integrity of decision making processes in decentralised organisations and platforms. Traditional voting systems often struggle with scalability and privacy issues, especially when trying to verify votes without compromising voter anonymity.
Merkle trees offer a sophisticated solution to these challenges. By structuring votes within a Merkle tree, the system can efficiently verify that a vote has been included without exposing all individual votes. Voters submit their votes, which are hashed and added as leaf nodes in the tree. The Merkle root is then published, serving as a commitment to the entire set of votes.
Below is a basic example of a voting contract utilising Merkle trees:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
import "@openzeppelin/contracts/utils/cryptography/MerkleProof.sol";
contract MerkleVoting {
bytes32 public merkleRoot;
mapping(address => bool) public hasVoted;
uint256 public yesVotes;
uint256 public noVotes;
constructor(bytes32 _merkleRoot) {
merkleRoot = _merkleRoot;
}
function vote(bool _vote, bytes32[] calldata merkleProof) external {
require(!hasVoted[msg.sender], "Already voted");
bytes32 leaf = keccak256(abi.encodePacked(msg.sender));
require(
MerkleProof.verify(merkleProof, merkleRoot, leaf),
"Invalid Merkle proof"
);
hasVoted[msg.sender] = true;
if (_vote) {
yesVotes += 1;
} else {
noVotes += 1;
}
}
}This contract again uses the OpenZeppelin MerkleProof.sol library to create a voting system where users get to vote if they are included in the Tree. Quite fitting for an election year with much debate about election fraud and ID based voting.
Case Study 3. Merkle Trees In Layer 2 Rollups
As blockchain networks grow, scalability becomes a pressing issue. Layer 2 solutions, such as rollups, aim to address this by processing transactions off-chain and submitting summarised data back to the main chain. Merkle trees are instrumental in enabling these solutions.
In rollups, batches of transactions are aggregated off-chain, and a Merkle root representing these transactions is computed. This root is then submitted to the main chain, where it acts as a cryptographic commitment to the batch of transactions. Users can interact with the rollup by providing Merkle proofs that their transactions are included in the batch.
Below is a simplified example illustrating how a Layer 2 rollup might interact with a smart contract using Merkle trees:
// SPDX-License-Identifier: MIT
pragma solidity ^0.8.0;
contract MerkleRollup {
bytes32 public stateRoot;
event StateRootUpdated(bytes32 indexed newRoot);
function updateStateRoot(bytes32 _newRoot) external {
// Only authorised entities should be allowed to call this function
// For simplicity, access control is omitted
stateRoot = _newRoot;
emit StateRootUpdated(_newRoot);
}
function verifyInclusion(
bytes32 leaf,
bytes32[] calldata merkleProof
) external view returns (bool) {
// Verify the Merkle proof against the current state root
return verifyProof(leaf, merkleProof, stateRoot);
}
function verifyProof(
bytes32 leaf,
bytes32[] memory proof,
bytes32 root
) internal pure returns (bool) {
bytes32 computedHash = leaf;
for (uint256 i = 0; i < proof.length; i++) {
bytes32 proofElement = proof[i];
if (computedHash <= proofElement) {
// Hash(current computed hash + current element of the proof)
computedHash = keccak256(
abi.encodePacked(computedHash, proofElement)
);
} else {
// Hash(current element of the proof + current computed hash)
computedHash = keccak256(
abi.encodePacked(proofElement, computedHash)
);
}
}
// Check if the computed hash (root) is equal to the provided root
return computedHash == root;
}
}
Users can interact with this overly simplified contract to verify whether a specific transaction or piece of data has been included in the current state by providing a Merkle proof.
The verifyInclusion function checks whether the transaction or state (represented as a leaf node in the Merkle tree) is part of the batch by comparing the Merkle proof with the current root stored on-chain. The contract uses a helper function verifyProof, which reconstructs the Merkle root from the provided proof and leaf, ensuring that it matches the stored root.
This process allows for efficient on-chain verification of off-chain transactions or transactions happening on a different chain, reducing the need for extensive data storage and computation on Ethereum mainnet. It ensures that users can trust the rollup’s validity by providing cryptographic proof without overwhelming the network with large amounts of data, improving scalability while maintaining security.
Merkle trees have proven to be a versatile and powerful tool in the development of blockchain technologies and decentralised applications. Their ability to enable efficient verification of large data sets and provide proofs of inclusion without revealing entire data sets addresses some of the fundamental challenges in these systems.
From facilitating secure and cost effective airdrops to enhancing the scalability and privacy of voting mechanisms, and underpinning the efficiency of Layer 2 rollups, Merkle trees are at the heart of innovative solutions in the blockchain ecosystem.


